5.13 浮遊電極

電圧の異なる2個以上の電極を入力すると計算領域全体に電圧分布が発生します。 この中に金属を置くと何らかの電圧を持った電極となりますが、 その電圧は未知なので電極として入力することができません(浮遊電極)。
このとき浮遊電極の電圧を求めるには浮遊電極の電圧を変えて計算を行い、 ost.logに出力される全静電エネルギーが最小になるケースを探します。
リスト5-13-1に入力データを示します。
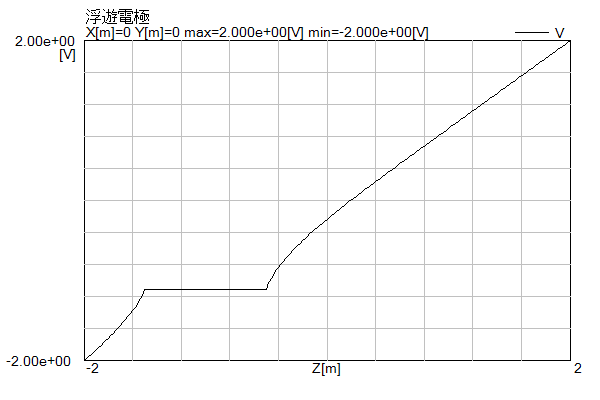
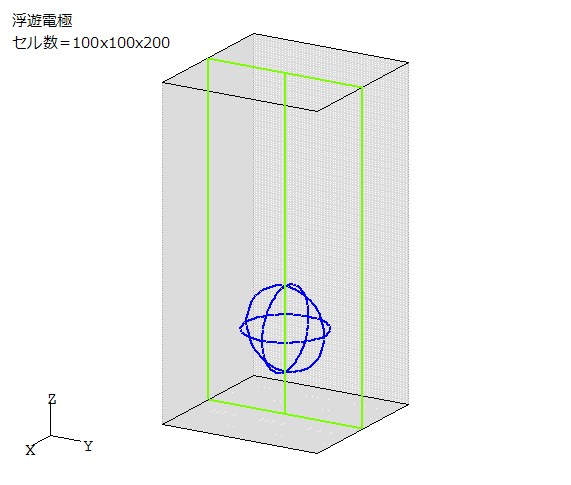
図5-13-1に形状出力図を示します。 2個の電極(下が-2V、上が+2V)と1個の球状の浮遊電極を置いています。

OpenSTF 1 6
title = 浮遊電極
xmesh = -1 100 1
ymesh = -1 100 1
zmesh = -2 200 2
volt = -2 
volt = 2 
volt = -1.1 
geometry = 1 1 1 -1 1 -1 1 -2 -2 
geometry = 1 2 1 -1 1 -1 1 2 2 
geometry = 1 3 2 -0.5 0.5 -0.5 0.5 -1.5 -0.5 浮遊電極
solver = 1.98 2000 100 0
plot1d = V Z 0 0
1ddb = 0
1dlog = 1
plot2d = V X 0
plot2d = E X 0
2dfigure = 1 1
2ddb = 0
2dcontour = 1
2dobject = 1 1
2dlog = 1
end

図5-13-1 形状出力図

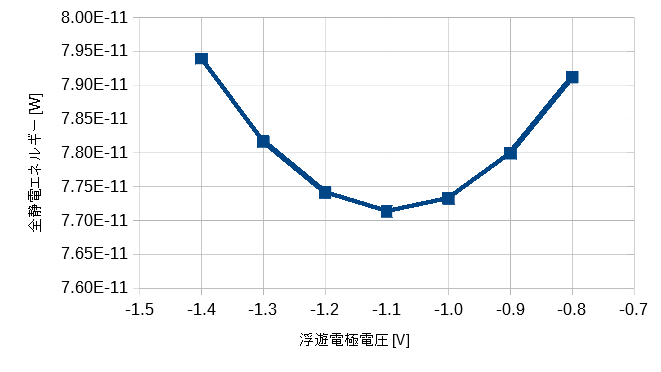
図5-13-2は浮遊電極の電圧を変えて計算を行い、全静電エネルギーをプロットした図です。
これから浮遊電極電圧=-1.1Vのとき全静電エネルギーが最小になることがわかります。

図5-13-2 浮遊電極電圧と全静電エネルギーの関係

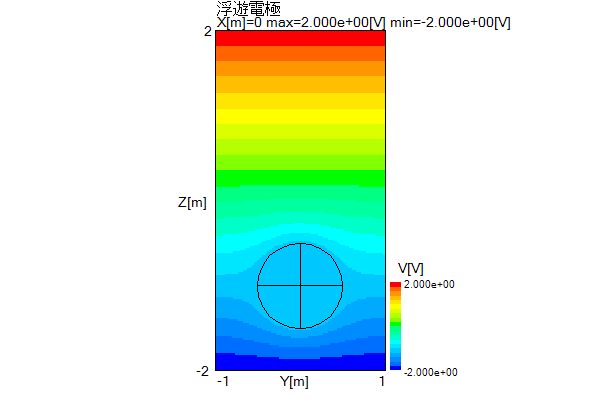
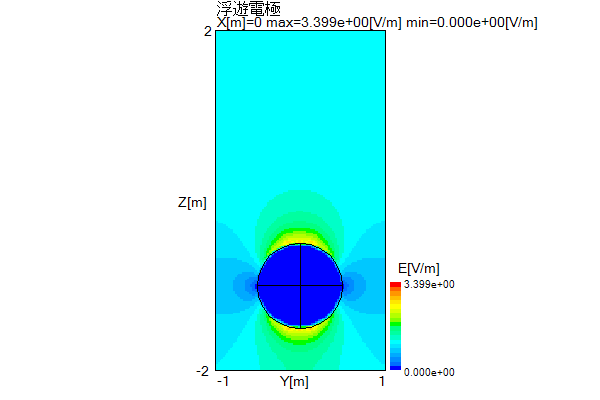
以下に上で求めた浮遊電極電圧のときの電圧・電界分布図を示します。 金属の中では電圧は一定であり、電界は0になります。

図5-13-3 電圧線上分布図(X=Y=0線)

図5-13-4 電圧面上分布図(X=0面)

図5-13-5 電界面上分布図(X=0面)