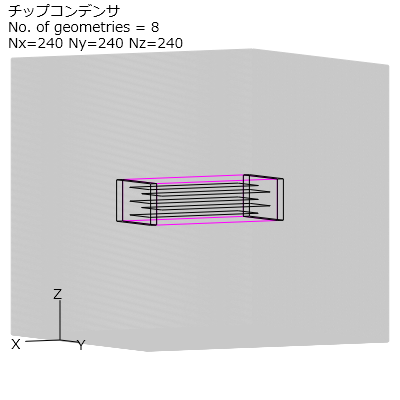
図5-11-1 形状出力図
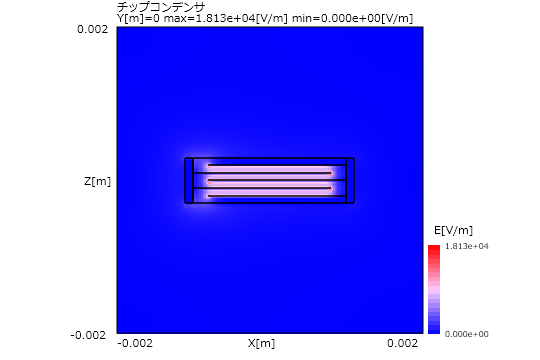
図5-11-2 電界面上分布図
チップコンデンサーを計算します。
リスト5-11-1に入力データを示します。
図5-11-1に形状出力図を示します。
誘電体の両側を電極で挟み、それぞれの電極から交互に平板電極が広がっています。
図5-11-2に電界の面上分布図を示します。電極間に大きな電界が発生していることがわかります。
数値出力ost.logから電極上の電荷は3.24465e-12[C]となり、
これからコンデンサの容量は C=Q/V=3.24pFとなります。
一方容量の公式からは
C = ε0 * εr * 電極面積 * (電極枚数 - 1) / 電極間距離
= 8.854e-12 * 10 * (1.6e-3 * 0.6e-3) * (5 - 1) / 0.1e-3 = 3.40pF
となり近い値になります。
OpenSTF 1 3 title = チップコンデンサ xmesh = -0.002 240 0.002 ymesh = -0.002 240 0.002 zmesh = -0.002 240 0.002 volt = 0 volt = 1 epsr = 10 geometry = 2 1 1 -0.001 0.001 -0.0005 0.0005 -0.0003 0.0003 geometry = 1 1 1 -0.0011 -0.001 -0.0005 0.0005 -0.0003 0.0003 geometry = 1 2 1 0.001 0.0011 -0.0005 0.0005 -0.0003 0.0003 geometry = 1 2 1 -0.0008 0.001 -0.0003 0.0003 0.0002 0.0002 geometry = 1 2 1 -0.0008 0.001 -0.0003 0.0003 0 0 geometry = 1 2 1 -0.0008 0.001 -0.0003 0.0003 -0.0002 -0.0002 geometry = 1 1 1 -0.001 0.0008 -0.0003 0.0003 0.0001 0.0001 geometry = 1 1 1 -0.001 0.0008 -0.0003 0.0003 -0.0001 -0.0001 solver = 1.99 3000 100 1e-5 plot2d = V Y 0 plot2d = E Y 0 2dfigure = 1 0 2ddb = 0 2dobject = 1 1 2dlog = 1 window2d = 750 500 15 window3d = 500 500 60 30 end

図5-11-1 形状出力図

図5-11-2 電界面上分布図