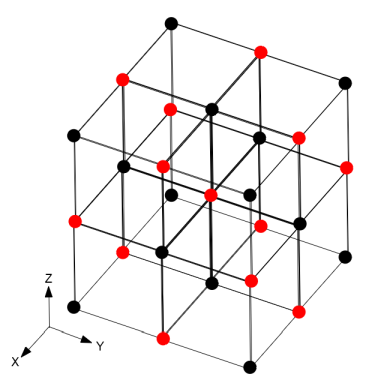
図2-4-1 red-black SOR法
本シミュレーターではSOR法を並列化する手法としてred-black法を採用します[4]。
これは行列の性質を利用して並列計算する方法です。odd-even法と呼ぶこともあります。
式(2-2-4)からわかるように変数の更新を並列に実行すると変数への参照が競合し結果に再現性がありません。
ところが式(2-1-6)を見ると、自分以外はi,j,kのいずれかが1だけ異なる変数を参照しています。
これから各反復計算の第1ステップではi+j+kが偶数となる変数のみを更新し、
続いて第2ステップではi+j+kが奇数となる変数のみを更新します。
図2-4-1で説明すると、黒丸を更新するときは自分自身と赤丸を参照し、
赤丸を更新するときは自分自身と黒丸を参照します。
黒丸のi+j+kの偶奇はすべて同じあり、赤丸のi+j+kの偶奇はすべて同じです。
以上の方法によって変数の競合がなくなり、スレッド数によらず並列計算で同じ結果が得られます。
反復回数当たりの計算量も変わりません。
