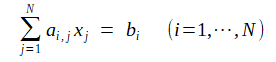2.2 SOR法による連立一次方程式の解法

2.2.1 連立一次方程式の解法

前節の離散式(2-1-6),(2-1-9),(2-1-10)をまとめると次式の連立一次方程式になります。

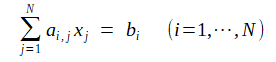(2-2-1)

連立一次方程式の解法には直接法と反復法があります。
直接法は主に密行列(行列要素がほとんど非0である行列)で用いられます。 LU分解法が代表的なものです。密行列は境界要素法などで現れます。
反復法は主に疎行列(各行の非0の行列要素が少数個である行列)で用いられます。 共役勾配法とSOR法(successive over-relaxation method, 逐次的過剰緩和法)[3][4][5]が代表的なものです。疎行列は差分法などで現れます。
本シミュレーターは差分法を用いているために反復法を採用します。 共役勾配法はたくさんの作業配列が必要となり必要メモリーが増えますが、 SOR法は作業配列が不要であるために最小限のメモリーで計算することができ、 従って大規模問題を解くことができます。 以上の理由から本シミュレーターではSOR法を採用します。

2.2.2 反復法

ここでは各種の反復法を説明します。
反復法では適当な初期値x_i⁽⁰⁾を与えて解が収束するまで計算を繰り返します。 ここで右上の数字は反復回数を表します。

Jacobi法
Jacobi法のアルゴリズムは次式の通りです。 更新した解を別途保存しておき最後にすべての変数を更新します。 この方法はメモリーが2倍になる欠点があります。

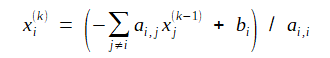(2-2-2)

Gauss-Seidel法
Gauss-Seidel法のアルゴリズムは次式の通りです。 変数をその都度更新します。このために余分な配列が不要になりプログラミングも簡単になります。

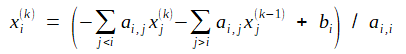(2-2-3)

SOR法
SOR法のアルゴリズムは次式の通りです[3][4][13]。 いったんGauss-Seidel法と同じ式で計算し、さらに緩和係数ωで外挿します。 ωを加速パラメーターと呼ぶこともあります。 1≦ω<2の範囲で使用します。 ωが2に近いとき最も収束が速くなります。ω=1のときはGauss-Seidel法と一致します。 SOR法はGauss-Seidel法と同じ演算量で収束を速くする優れたアルゴリズムですが、 最適なωを予め知ることができないという欠点があります。

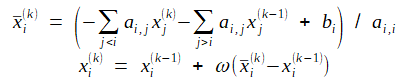(2-2-4)

2.2.3 行列の特徴

本シミュレーターの行列については以下の特徴があります。

• 右辺ベクトルはゼロベクトルです。b=0
• 電極では電圧は既知であるために、電極上の節点は計算する必要がありません。
• 各行の要素の和が0です(Σ_ja_i,j= 0)。 広義の対角優位行列に分類されます。[3]

2.2.4 反復計算の初期値

方程式は電圧について線形なので電圧を一次変換しても行列は変わりません。 電極電圧の最大値をV_max、最小値をV_minとします。 反復計算の初期値を次式で与えます。 これによって最大電圧=+1、最小電圧=-1と正規化されて無次元量になりますので、 電極の電圧によらず収束状況が一定になります。

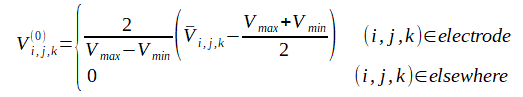(2-2-5)

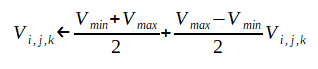(2-2-6)

2.2.5 収束判定条件

収束判定条件は次式とします。ここでεは十分小さい数です。 左辺のr^(k)を残差(residual)と呼びます。

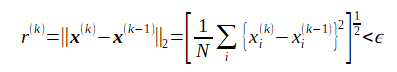(2-2-7)

2.2.6 反復法の収束の比較

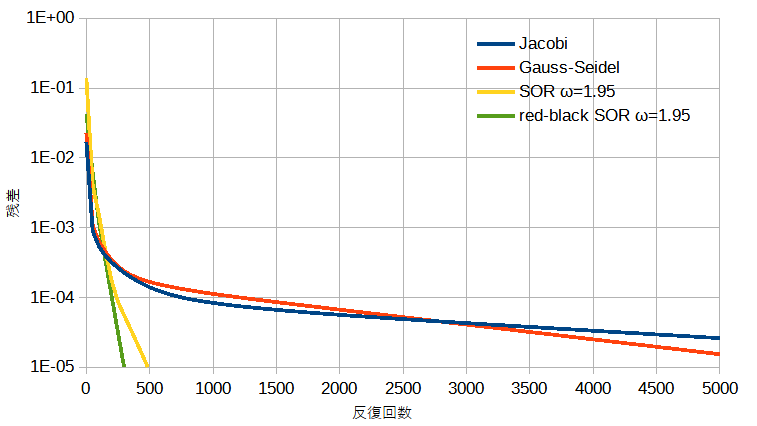
2.2.2で述べた各種の反復法の収束状況を比較します。
問題図は図2-2-1の通りです。セル数=100*100*100です。

図2-2-1 ベンチマーク問題

図2-2-2 反復法の各手法の収束状況（Nx=Ny=Nz=100）

2.2.7 単精度と倍精度

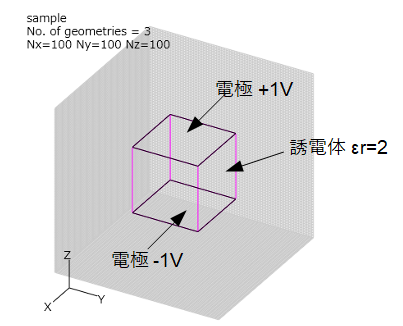
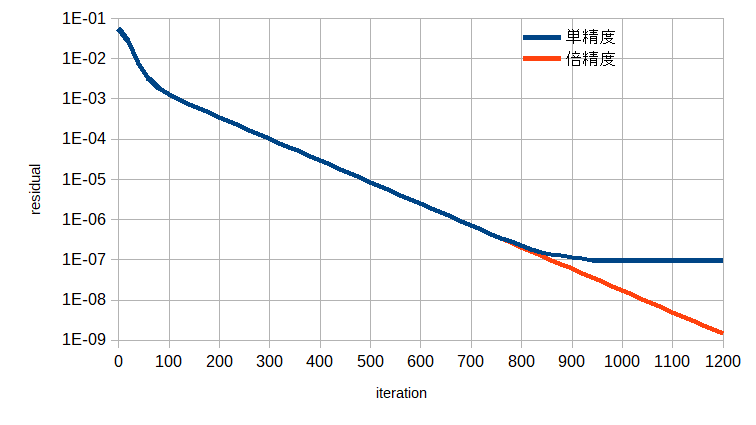
本シミュレーターではGPUで計算を行うことも考慮して単精度で計算します。 図2-2-3に単精度と倍精度の収束状況を示します。 実用上は収束判定条件は1e-5で十分なので単精度で問題ないことがわかります。

図2-2-3 単精度と倍精度の収束状況(red-black SOR法, ω=1.95, Nx=Ny=Nz=100)

2.2.8 必要メモリー

計算に必要な配列は各節点における電圧と比誘電率と電極情報です。
計算時間と必要メモリーの観点から以下の2種類のモードを考えます。 名前の由来は(2)がベクトル計算機に適合していることによります。
(1) novectorモード
誘電体の比誘電率の種類と電極の電圧の種類を255通り以下に限定し、 比誘電率と電圧への参照を間接的な参照とします。 これによりそれぞれ1バイトで済み、計算に必要なメモリーは6*Nx*Ny*Nzバイトとなります。 例えばNx=Ny=Nz=1000のとき6GBです。
(2) vectorモード
誘電体の比誘電率と電極の電圧を直接的な参照とします。 計算に必要なメモリーは12*Nx*Ny*Nzバイトとなります。 例えばNx=Ny=Nz=1000のとき12GBです。

2.2.9 緩和係数

図2-2-4に緩和係数ωを変えたときの収束状況を示します。 ωが2に近づくほど収束が速いことがわかります。

図2-2-4 緩和係数と収束状況の関係(red-black SOR法, Nx=Ny=Nz=100)

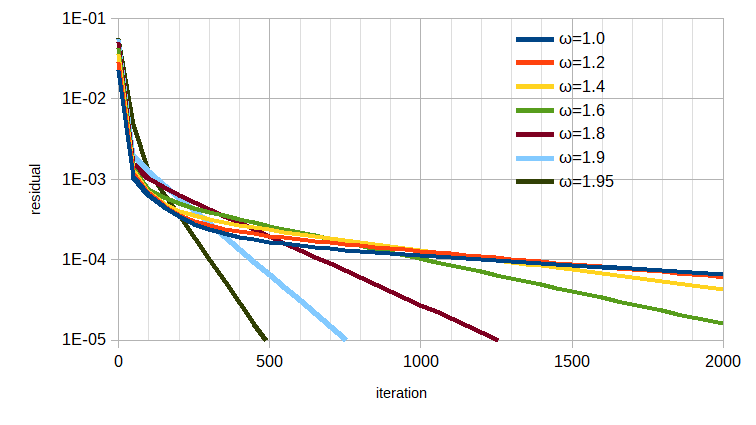
収束付近(残差=1e-5付近)では反復回数と残差の対数が直線関係にありますので、 収束の速さは指定した残差(例えば1e-5)に達する反復回数で評価することができます。

2.2.10 セル数と最適緩和係数の関係

ここでは収束が最も速くなる緩和係数を最適緩和係数と呼びω_optと表します。 上で述べたように最適緩和係数は予め知ることができません。 最適な緩和係数を知るために複数回の計算を行うことは無意味ですので、 最適緩和係数のおおよその値を求める式があれば便利です。
図2-2-5はセル数(Nx X Ny X Nz)をいろいろ変えたときの、緩和係数ωと収束するまでの反復回数の関係です。 収束反復回数が最小になる緩和係数が最適緩和係数ω_optです。 図からセル数が大きくなると最適緩和係数ω_optも大きくなることがわかります。

図2-2-5 セル数と最適緩和係数の関係(red-black SOR法, 収束判定条件=1e-5, 矢印は式(2-2-8))

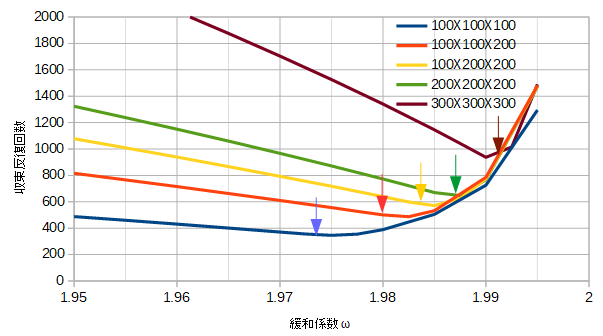
図2-2-5に次式で評価される最適緩和係数ω_optを矢印で示しています。 これから次式は最適緩和係数ω_optのよい近似値であることがわかります。

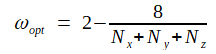(2-2-8)